(More topics to follow)

Suppose you drive your car into a lake. 

It typically takes about 10 minutes for the electrics to fail in a submerged car, but you are unlucky in this respect. You find that you cannot open your window. The car sinks and comes to rest so that the bottom of its wheels are 2m under water. Use your knowledge of hydrostatic pressure (the fact that the pressure on a submerged object is given by pgd, where g is acceleration due to gravity, d is the depth of the object, and p is the density of the fluid) to determine if you can open the door.

1. Model the shape of your car (i.e. come up with sensible functions/shapes which you can apply calculus to). Then calculate the total pressure on the door if it is completely submerged, with the bottom of the door exactly two metres below the surface of the lake.
2. Can you open the door by kicking it? Probably not... estimate the amount of force you (and/or your companion) are able to apply, perhaps by using the leg press in the weight room in the El Pomar centre. Ignore the effects of torque about the hinges. Just see if you can budge the door.
3. While doing these calculations you miss your opportunity to escape. As the car fills up with water and you anticipate a watery end to your life, you realize that the pressure from water inside the door will begin to equalize the pressure from the outside. You will have another chance to get out! How much water do you need to let into the car before you can open the door (i.e. how high should the water level be against the inside of the door)?
4. P.S. Any thoughts about the sunroof? Don't forget to take off your seatbelt!

This project deals with custom made gold wedding bands. Its shape is obtained by revolving the region shown about a horizontal axis. The resulting band has Inner radius R, Minimum Thickness T, Width W.

The curved boundary of the region is an arc of a circle whose center lies on the axis of revolution. For a typical wedding band with given dimensions R, T, W, the jeweller must first calculate the volume of the desired wedding band to determine how much gold will be required.

Suppose that the jeweller plans to charge the customer $100 per troy ounce of allow (90% gold and 10% silver) used to make the ring. The profit on the sale, covering the jeweler's time and overhead in making the ring, is fairly substantial because the price of gold is generally under $400 per ounce and that of silver under $5 per ounce. The inner radius of the wedding band is determined by the measurement of the customer's finger (in millimeters); there are exactly 25.4 mm per inch. Suppose that the jeweller makes all the wedding bands with T = 1. Then for a given acceptable cost C (in dollars) the customer wants to know the maximum width W of the wedding band he can afford.

You will need to know that the density of the gold silver allow is 18.4 g/cm³ and that 1 lb = 453.59 g contains 12 troy ounces.

1. Show that the volume V is given by the formula If these measurements are in mm, then the units of V are in mm³; there are 1000mm³ in 1cm³.
2. Measure your own ring finger to determine R (you can measure its circumference C with a piece of string and then divide by 2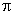). Then choose a cost figure C in the $100 to $1000 price range. Fix a width W of the band that costs C dollars (at $1000/oz).
3. Use Mathematica or some computational aid to solve the resulting cubic equation.

Extra: Since this problem is shorter than the others, calculate this additional volume: the intersection of two pipes which are cylinders of radius 2, as shown:

The Chinese Mathematician Liu Hui (third century AD) tried to find this volume and failed. He wrote this poem called 'Box-Lid'. (Note that the rhyming is lost in translation)

Look inside the cube
And outside the box-lid;
Though the dimension increases,
It doesn't quite fit.
The marriage preparations are complete;
But square and circle wrangle,
Thick and thin are treacherous plots,
They are incompatible.
I wish to give my humble reflections,
But fear that I will miss the correct principle;
I dare to let the doubtful points stand,
Waiting
For one who can expound them.

Spruce Budworms are a serious problem in Canadian forests. Budworm 'outbreaks' can occur in which balsam fir trees are quickly defoliated by hordes of ravenous budworms. A model of budworm population leads to the differential equation

where y is the number of budworms in tens of thousands in a certain area, and k is a positive parameter associated with birth and death rates. An 'outbreak threshold' for y is a positive number y* such that

• y(t) is decreasing if y(0) is slightly less than y*
• y(t) is increasing if y(0) is slightly more than y*

Note that the equation is essentially logistic with the additional termrepresenting the rate at which the worms are eaten by predatory birds.

1. Choose A = 1. Graph the right hand side of the differential equation for several values of k. What are the possibilities for the numbers of positive roots?
2. For three different values of k (for example, k = 0.3, 0.45, and 0.6), plot the direction field of the differential equation for t [0,20] and y [0,10]. Also, use Euler's method to plot approximate solution curves with intial values y(0) = 1, 3, and 10 for each choice of k. What happens to each solution as ?
3. For which values of k in the previous part is an outbreak possible? What is the outbreak threshold of y in each case?
4. Find the values of k for which the right hand side of the equation has a double root (set the right side equal to zero and solve simulataneously with f'(y) = 0 for y.) Then repeat the second part with this value of k.
5. What happens to your solutions if you increase A from 1 to 10 (i.e. if you introduce more/hungrier birds).
6. Conclude with a report on the precise values of k for which a budworm outbreak is possible, and the effects of bird predation. How can the budworms be most effectively controlled?

Do the laboratory exercise on page 648 form chapter 10. Use Mathematica to obtain your plots.

1. See me for hints about deriving the equation for the hypocycloid.
2. The Mathematica commands which you will need: Plotting a parametric curve, for example a circle:

x[t_{_}] = Cos[ t ]
x[t_{_}] = Sin[ t ]
ParametricPlot[{ x[ t ], y[ t ] }, {t, 0, 2Pi}]

or


x[t_{_}] = Cos[ t ]
x[t_{_}] = Sin[ t ]
ParametricPlot[{ x[ t ], y[ t ] },{t,0,2Pi},
PlotStyle -> { Thickness[.01], SlateBlue}]



3. You may need to use a range of t values which go through several multiples of 2 in order to see the entire hypocycloid.
4. This question is interesting! Think about it carefully!
5. The equation for the epicycloid is

The argument to show this is similar to the one you used in part 1. Stop by if you need hints!

Project Five

Modelling the US Population

1. Exponential model: Use the model dP/dt=kP for exponential population growth to obtain  P=Po e^kt, where Po is the initial population.
2. Refer to the data at the top in the table. Take t=0 to be the year 1790, and let t be measured in years. Use the data from t=0 (1790) and t=10 (1800) to determine a value for k.
3. Use your solution to predict population size each decade after 1790 until you reach the year 1930. \For which years is your prediction reasonable? Discuss this.
4. Solve the logistic equation as outlined in section 9.5 of the text. Show the details such as how the intergration by partial fractions is carried out.
5. Use a logistic model and the data from the 1860, 1870 and 1880 censi to decide on the constants to use. What population levels do you predict for the years 1860 through 1930?
6. What can you find out about more current trends in population growth in the US?

How the projects will be graded:

For your write up, focus on communicating your methods and results to an intelligent audience whose knowledge of mathematics does not go beyond calculus two. Your project should consist of a) prose which describes the general background for the problem, the methods, and the conclusions with references throughout to b) a set of detailed calculations supporting your claims. (Label each computation and refer to it clearly in the prose). The prose component should be typed. It is highly recommended that you write the calculations by hand. Your grade for your mathematical method will be based almost entirely on this part, so it is important that you don't skip details and steps here. You do not necessarily have to follow the structure a, b, c, d, e etc. in the order outlined in the topic you choose. Just make sure you cover each point thoroughly. Correct spelling, grammar and usage of mathematical terms, notation and principles will .Your grade out of 41 points will be based on the following categories:

Mathematical Method: 20 points
Use the methods you've learnt in class so far ... correctly!

Layout: 5 points
As described above

English: 5 points
Use English to clearly and effectively communicate your methods and conclusions. The spell/grammar check is just a beginning ....

Mathematical Notation: 5 points
Use correct notation, positioning of the `=' sign etc.

Background: 5 points
Give clear background information or invent a story to give a context for your project.

References:1 point
Include a list of references, if relevant, including internet sites.

Extra Credit: up to 3 points
Any imaginative ideas and mathematical/artistic additions which extend the topic in some (tasteful) way.