Monte Carlo Simulation Quiz
In this exercise you will use Monte Carlo methods to estimate the value of \(\pi\). The diagram below shows circle inside a square.
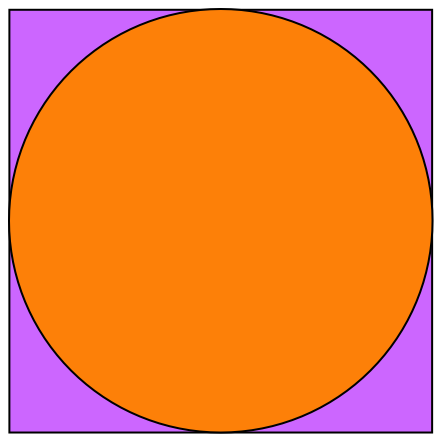
If the circle has a radius \(r\) then its area is \(A_c = \pi r^2\), and the square's area is \(A_s = 4 r^2\). The ratio of the areas is $$ \frac{A_c}{A_s} = \frac{\pi}{4} \implies \pi = 4 \frac{A_c}{A_s}. $$ If we randomly generate a set of \((x,y)\) coordinates inside the square, the number of those points inside the circle will be proportional to area of the circle so that $$ \frac{A_c}{A_s} = \frac{N_C}{N_\mathrm{total}}, $$ where \(N_C\) is the number of points that lie in the circle and \(N_\mathrm{total}\) is the total number of points. An estimate for \(\pi\) is therefore $$ \pi_\mathrm{est} = 4 \frac{N_C}{N_\mathrm{total}}. $$ Write a function that takes \(N_\mathrm{total}\) as an input parameter and returns an estimate for \(\pi\). Use this function to estimate \(\pi\) for \(N_\mathrm{total} = 10\) to \(10^7\). Use semilogx()1 to plot the estimated value of \(\pi\) as a function of \(N_\mathrm{total}\). The estimated values of \(\pi\) should become more accurate as \(N_\mathrm{total}\) increases.